Leaderboard

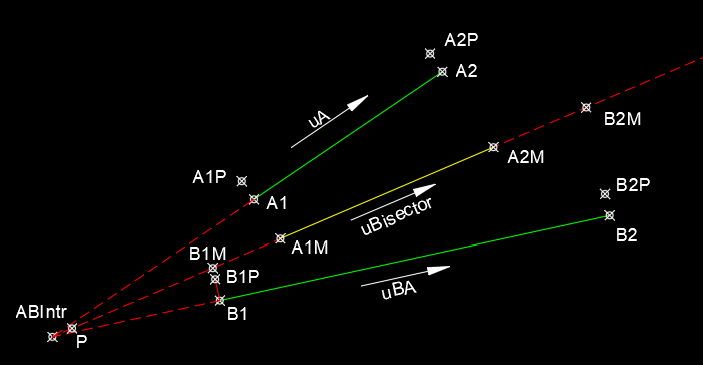
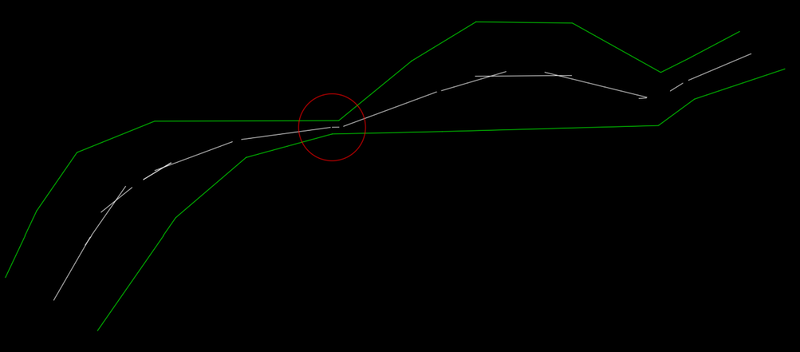
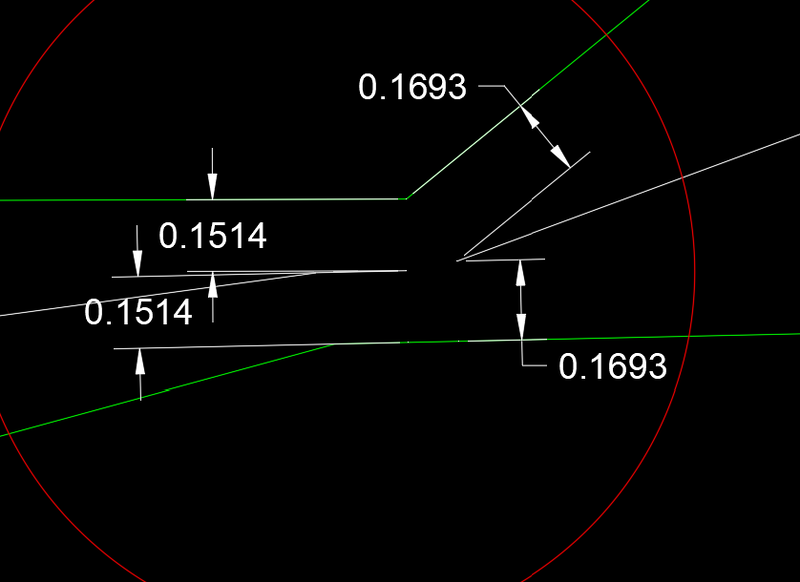
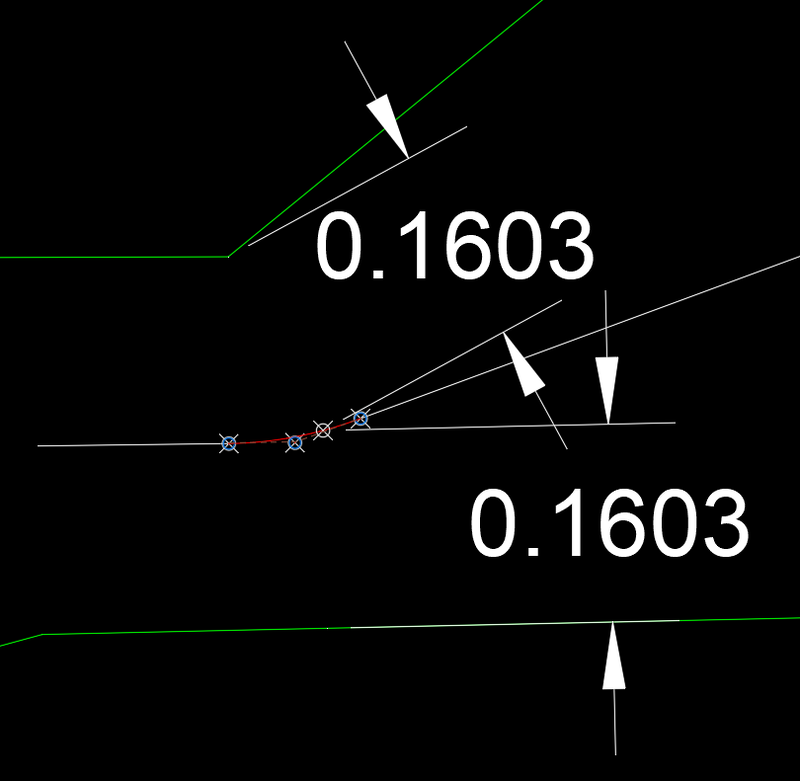
[code edited 11/3/2025] I have enjoyed the discussion of this thread. As I gave the task more thought and anaysis it became more clear that the task was not simple. As it appears that there is still no satisfacory solution I thought I would offer the following. The first goal for me was to create a function that would create a midline between two non parallel lines. The mid-lines extents should be a function of the given line segments. This function could then be used in a program that would step through the line segments of one of the polylines and search the other polyline for relevant segments. The function "midline" accepts four points. The first two points, A1 and A2, are the ends of one line sement while the thrid and fourth points, B1 and B2, are the ends of an opposing ilne segments. The diagram below details the variables in the function. The program uses vectors as I prefer them over angles which present, for me, a variety of problems. uA = unit vector in the diection from A1 to A2 uB = unit vector in the direction from B1 to B2 uBisector = unit vector in the direction of the angle bisector of uA and UB The ends of the two lines are projected onto the bisecting line defining 4 points, A1M, A2M, B1M, B2M. I debated which of the points to output for the line to be drawn. I first used the closest and furthest points from the intersecttion point ABIntr but I found it more helpful to use the two intermediate points (A1M and A2M in the example above). Here's an example of the results after manually steppng alone the polyline. Looking at the area circled in red we find: To fill the gap we need a curve that starts with a radius of 0.1514 and ends with a radius of 0.1693. This can be done with a spline or you may find it acceptable to extend the two lines to the point of intersection. The best way to create the spline is to use the Control Vertex Method and use the two endpoints and the imaginary point of intersecton for the middle CV. This ensures tangency to the two lines. As can be seen below the distance to a random point along the spline (red) agree! Run the program "test" and specify the end points of a line segment on one of the polylines, then the endpoints on a line segment on the opposing polyline. I have found the results very accurate and although it may not be used for creating the complete "hybrid " polyline it is helpful in finding the correct line for a specific segment. ;;---------------------------------------------------------------------------- ;; Determines the endpoints of a line the is midway between two lines defined by their end points. ; Input: 4 points, the ends of the first line followed by the ens of the second line ; Output: a list containing the two point of the midline if there's a solution and nil if no solution ; L. Minardi 10/31/2025 - Revised 11/3/2025 (defun midLine (a1 a2 b1 b2 / ua ub p vp d s a1m a2m b1m b2m d1 d2 d3 d4 slist a1p a2p b1p b2p m1 m2 mmid mp) (setq ua (unitVecAB a1 a2) ub (unitVecAB b1 b2) ) (if (< (dot ua ub) 0.0) (setq ub (mapcar '* ub '(-1 -1 -1))) ) (if (> (abs (dot ua ub)) 0.9999) ; are lines parallel? (progn ; lines are parallel (setq p (mapcar '/ (mapcar '+ a1 b1) '(2 2 2)) ; point on midline vp (list (- (cadr ua)) (car ua) 0.0) ; vector perpendicular to ua d (/ (dot (mapcar '- b1 a1) vp) 2.0) ; distance to midline s (dot (mapcar '- a1 p) ua) a1m (mapcar '+ p (mapcar '* ua (list s s s))) s (dot (mapcar '- a2 p) ua) a2m (mapcar '+ p (mapcar '* ua (list s s s))) s (dot (mapcar '- b1 p) ua) b1m (mapcar '+ p (mapcar '* ua (list s s s))) s (dot (mapcar '- b2 p) ua) b2m (mapcar '+ p (mapcar '* ua (list s s s))) d1 0.0 d2 (dot ua (mapcar '- a2m a1m)) d3 (dot ua (mapcar '- b1m a1m)) d4 (dot ua (mapcar '- b2m a1m)) ) (setq slist ; sorted list of distances (vl-sort (list (list a1m d1) (list a2m d2) (list b1m d3) (list b2m d4)) (function (lambda (e1 e2)(< (cadr e1) (cadr e2)))))) ; use the middle two mid point from the line (setq m1 (car (nth 1 slist)) m2 (car (nth 2 slist)) ) (setq mmid (mapcar '/ (mapcar '+ m1 m2) '(2 2 2))) (setq mp (* (dot (mapcar '- a1m mmid) (mapcar '- a2m mmid)))) (if (<= mp 0) (setq theLine (list m1 m2)) (setq theline nil) ) ;;;;; ) ) ; end lines parallel (progn ; lines are not parallel (setq ABIntr (inters A1 A2 B1 B2 nil)) (setq p (mapcar '+ ABIntr (mapcar '/ (mapcar '+ ua ub) '(2 2 2))) ;(setq p (mapcar '+ ABIntr (mapcar '/ (mapcar '+ a1 b1) '(2 2 2))) uBisector (unitVecAB ABIntr p) vp (list (- (cadr ua)) (car ua) 0.0) A1p (mapcar '+ A1 vp) a1m (inters A1 A1P ABIntr p nil) A2p (mapcar '+ A2 vp) a2m (inters A2 A2P ABIntr p nil) vp (list (- (cadr ub)) (car ub) 0.0) B1p (mapcar '+ B1 vp) B1m (inters B1 B1P ABIntr p nil) B2p (mapcar '+ B2 vp) B2m (inters B2 B2P ABIntr p nil) d1 (distance ABIntr a1m) d2 (distance ABIntr a2m) d3 (distance ABIntr b1m) d4 (distance ABIntr b2m) ) (setq slist (vl-sort (list (list a1m d1) (list a2m d2) (list b1m d3) (list b2m d4)) (function (lambda (e1 e2) (< (cadr e1) (cadr e2))))) ) (setq m1 (car (nth 1 slist)) m2 (car (nth 2 slist)) ) (setq mmid (mapcar '/ (mapcar '+ m1 m2) '(2 2 2))) (setq mp (* (dot (mapcar '- a1m mmid) (mapcar '- a2m mmid)))) (if (<= mp 0) (setq theLine (list m1 m2)) (setq theline nil) ) ) ; end lines not parallel ) ; end if ) ; test function (defun c:test ( / a1 a2 b1 b2 mline ) (setq a1 (getpoint "\nEnter start point of first line: ") a2 (getpoint a1 "\nEnter end point of first line: ") b1 (getpoint "\nEnter start point of second line: ") b2 (getpoint b1 "\nEnter end point of second line: ") mline (midline a1 a2 b1 b2) ) (if mline (command "_line" "_non" (car mline) "_non" (cadr mline) "") (princ "\nNo Solution!") ) (princ) ) ; unit vector from point A to point B (defun unitVecAB (A B / x) (setq x (distance A B) x (mapcar '/ (mapcar '- B A) (list x x x)) ) ) ; dot product of vectors A and B (defun dot (A B / x) (setq x (mapcar '* A B)) (setq x (+ (nth 0 x) (nth 1 x) (nth 2 x))) );end of dot mid -poly.06.lsp